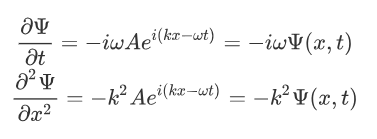Numerical approximations can be found for all other systems, assuming the equation is confined and, if large, that there are boundary conditions that allow computation within the timespan of the universe. To date, the only instance where an exact analytical (purely mathematical) solution to the unconfined Schrödinger equation has been found is in a single-electron system, e.g. By specifying the total energy ( Hamiltonian) of the quantum system, Schrödinger's equation can be solved, the solutions being quantum states. The Schrödinger equation is commonly written as an operator equation describing how the state vector evolves over time. The equation is named after physicist Erwin Schrödinger who proposed the equation in 1926. Schrödinger's equation is primarily applied to atomic and subatomic systems, such as electrons and atoms, but is sometimes applied to macroscopic systems (such as the whole universe). According to the Copenhagen interpretation of quantum mechanics, the state vector is used to calculate the probability that a physical system is in a given quantum state. In physics, especially quantum mechanics, the Schrödinger equation is an equation that describes how the quantum state of a physical system varies. For a non-technical introduction to the topic, please see Introduction to quantum mechanics.